Понимание обратных функций - важный аспект изучения математики в старших классах. Обратная функция - это функция, которая дает нам возможность восстановить исходную функцию, если мы знаем значения, полученные с помощью этой функции. Знание, как построить обратную функцию, может быть полезным при решении различных задач и упрощении вычислений.
Для построения обратной функции необходимо выполнить несколько шагов. Во-первых, определить, является ли исходная функция инъективной (инъекция означает, что каждому значению аргумента соответствует только одно значение функции). Если функция является инъективной, то полагаем, что она имеет обратную функцию.
Во-вторых, мы ищем формулу для обратной функции. Для этого приравниваем исходную функцию к переменной y и пытаемся выразить x через y. Если функция f(x) = y, то обратная функция обычно обозначается f^(-1)(y) или g(y).
В-третьих, мы проверяем, что полученная формула для обратной функции удовлетворяет требованиям, заданным в задаче. Для этого подставляем значения функции и аргумента в формулу и проверяем равенство полученных значений. Если полученная формула не удовлетворяет этим условиям, мы должны попытаться изменить формулу таким образом, чтобы она соответствовала требованиям задачи.
Что такое обратная функция?

В математике обратная функция существует только для некоторых функций, которые являются обратимыми. Обратная функция обозначается с помощью символа "^{-1}". Например, если имеется функция f(x), то её обратная функция будет обозначаться как f^{-1}(x).
Обратная функция является важным понятием в математическом анализе и применяется в различных областях науки и техники. Она позволяет решать уравнения, находить корни и находить значения, которые соответствуют определенным выходным значениям.
Для того, чтобы построить обратную функцию, необходимо соблюдать определенные условия. Функция должна быть однозначной, т.е. каждому значению входного параметра должно соответствовать только одно значение выходного параметра. Кроме того, функция должна быть обратимой, т.е. для неё должна существовать обратная функция.
Построение обратной функции может быть полезно в различных ситуациях, например, при решении уравнений, нахождении корней функции, построении графиков и других математических операциях.
Изучение понятия обратной функции поможет ученикам понять основные принципы функций и их преобразований, а также даст возможность применять эти знания на практике при решении различных задач и уравнений.
Важность обратной функции в математике
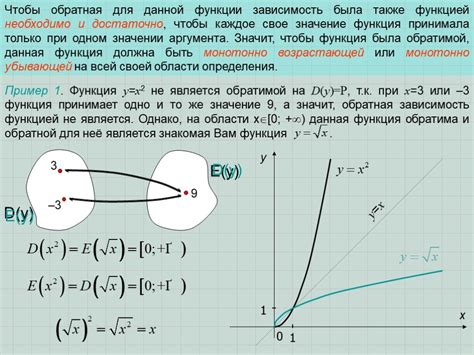
Обратные функции могут быть полезными в решении различных задач. Например, они помогают определить, какое значение аргумента соответствует определенному значению функции. Это может быть полезно при анализе данных, построении графиков и моделировании различных явлений.
Знание обратных функций также позволяет нам решать уравнения и системы уравнений. При решении уравнений обратная функция позволяет нам найти значения переменных, которые удовлетворяют заданному уравнению. Это помогает нам находить решения для различных практических задач.
Без знания и понимания обратных функций, многие математические задачи становятся гораздо сложнее или даже неразрешимыми. Поэтому освоение обратных функций является важным этапом в обучении математике. Оно помогает учащимся развивать логическое мышление, аналитические навыки и умение решать различные задачи.
В общем, обратная функция играет важную роль в математике и имеет большое практическое значение. Ее применение помогает нам понять и объяснить различные явления, а также решать разнообразные задачи. Поэтому изучение обратных функций является необходимым для получения полного представления о математике и ее приложениях.
Как определить, существует ли обратная функция?

Существует несколько условий, которые позволяют определить, существует ли у функции обратная:
- Функция должна быть инъективной (инъекция) или биективной (биекция). Если функция переводит разные аргументы в разные значения, то она является инъективной. Если функция еще и переводит каждое значение в уникальный аргумент, то она является биективной. Инъективная функция лишь позволяет понять, что аргументы, которые переводятся в разные значения, существуют. Биективная функция также позволяет восстановить значения аргументов по известным значениям функции.
- Для определенных классов функций существуют методы построения обратной функции. Например, если известно, что функция является линейной, то обратная функция будет иметь вид простой формулы, обратной функции.
- Некоторые функции могут быть приближены обратными функциями, например, при помощи разложения функции в ряд Тейлора. В таких случаях, обратная функция может быть найдена путем обращения коэффициентов в ряде Тейлора.
Если данные условия не выполняются, то обратную функцию построить невозможно или она может иметь сложный вид, который допускает неоднозначность.
График обратной функции и его особенности

Обратная функция представляет собой такую функцию, которая обращает действие исходной функции. Для построения графика обратной функции необходимо знать график исходной функции.
Особенностью графика обратной функции является то, что он представляет зеркальное отражение графика исходной функции относительно прямой y=x. Это означает, что значения оси x и y меняются местами.
Для построения графика обратной функции можно использовать таблицу значений, график исходной функции или выражение обратной функции.
На графике обратной функции могут быть определенные особенности, такие как:
| Особенность | Описание |
|---|---|
| Непрерывность | График обратной функции может быть непрерывным или иметь точки разрыва. Точки разрыва обратной функции соответствуют точкам разрыва исходной функции. |
| Монотонность | График обратной функции может быть монотонно возрастающим, монотонно убывающим или иметь участки монотонности. |
| Нахождение точек пересечения с осями | График обратной функции может пересекать оси координат в определенных точках. Например, точка пересечения с осью x соответствует точке пересечения графика исходной функции с осью y. |
| Асимптоты | График обратной функции может иметь вертикальные или горизонтальные асимптоты, которые определяются значениями функции на бесконечности. |
Построение графика обратной функции является важной темой в математике и помогает понять взаимосвязь между исходной функцией и ее обратной.
Примеры построения обратной функции
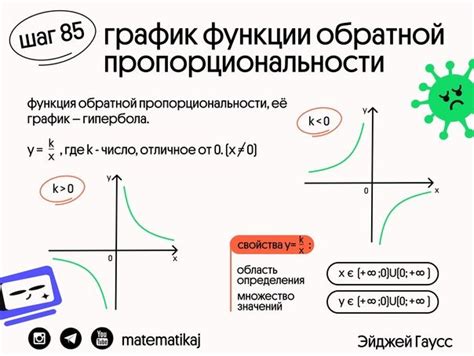
Рассмотрим несколько примеров построения обратной функции:
Пример 1:
Исходная функция: y = x + 5
Чтобы построить обратную функцию, нужно выразить x через y:
x = y - 5
Таким образом, обратная функция будет выглядеть следующим образом: y = x - 5
Пример 2:
Исходная функция: y = 2x
Для построения обратной функции нужно выразить x через y:
x = y / 2
Таким образом, обратная функция будет иметь вид: y = x / 2
Пример 3:
Исходная функция: y = x^2
Для построения обратной функции нужно найти корень из y:
x = √y
Обратная функция будет выглядеть следующим образом: y = x^2
Таким образом, при построении обратной функции необходимо установить соответствие между исходной функцией и ее обратной. Это позволяет находить исходные значения по известным результатам функции.
Свойства обратной функции
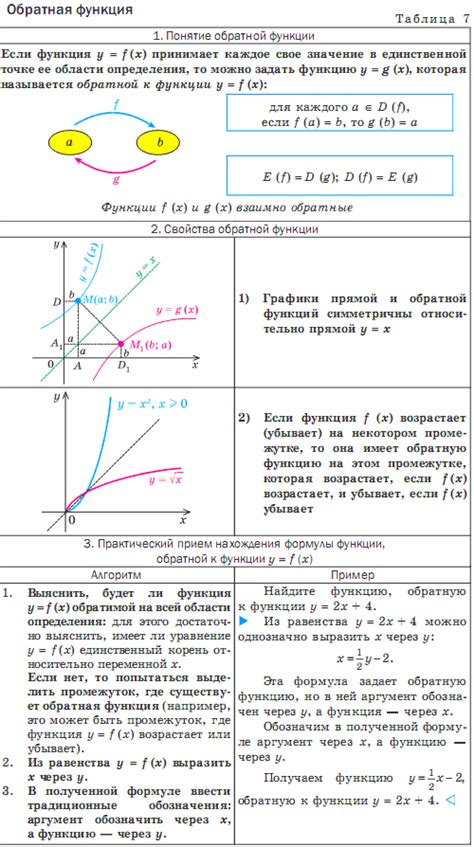
Обратная функция имеет несколько свойств, которые полезно знать при ее построении:
- Обратная функция обладает теми же значениями области определения и области значений, что и исходная функция.
- Обратная функция является симметричной относительно графика исходной функции относительно прямой y = x.
- Обратная функция описывает преобразование в обратном порядке, то есть, если исходная функция применяет операцию А, обратная функция применяет операцию, обратную А.
- Обратная функция дает единственный результат для каждого входного значения.
Построение обратной функции может быть полезно для решения различных задач, например, нахождение неизвестного значения при известном результате.
Однако, не все функции имеют обратные функции. Некоторые функции могут иметь обратную только в определенной области значений, или вообще не иметь обратной функции из-за потери информации.
Практические применения обратной функции в реальной жизни
Обратная функция играет важную роль в различных областях нашей жизни. Ниже представлены несколько примеров, где обратная функция находит свое применение:
- Криптография: Обратная функция используется для защиты информации и обмена сообщениями. Например, при шифровании данных используется функция, которая преобразует информацию в непонятный вид, а затем обратная функция позволяет вернуть данные в исходное состояние.
- Финансы: Обратная функция применяется при расчете различных финансовых операций, таких как проценты, кредиты, инвестиции и другие. Например, для расчета процентов по вкладу используется функция, а обратная функция позволяет узнать, сколько нужно вложить, чтобы получить определенную сумму.
- Медицина: Обратная функция применяется для анализа и обработки медицинских данных. Например, при измерении уровня лекарственного вещества в организме функция может преобразовать данные, а обратная функция позволяет получить исходные показатели.
- Транспорт: Обратная функция применяется для расчета времени и расстояния в пути. Например, при расчете времени в пути по известной скорости и расстоянию, функция может преобразовать данные, а обратная функция позволяет узнать скорость или расстояние при известном времени.
- Инженерия: Обратная функция используется при проектировании и моделировании различных систем и процессов в инженерии. Например, при расчете электрической мощности функция может преобразовать данные, а обратная функция позволяет узнать сопротивление или напряжение при известной мощности.
Все эти примеры показывают, насколько важна обратная функция в реальной жизни. Она позволяет нам решать различные задачи и применять математические концепции для практических целей.